It is amazing that light is actually an electromagnetic wave, but how can we actually “illuminate” this through mathematics? It was James Clerk Maxwell back in the 19th century who built upon his predecessors’ scientific observations of electric and magnetic fields and then applied mathematical analysis to these observations to enlighten us all about the true nature of light. We will start by briefly describing 4 of Maxwell’s physical laws and then show how applying mathematics to these laws results in shedding light on the nature of electromagnetic radiation. Finally, we will illuminate a very crucial identity used in the proof with respect to the curl of curl expression, and attempt to briefly discuss both its mathematical and intuitive meanings. The identity behind the curl of curl expression is very beautiful, both because of its elegant form and because, to me at least, it seems to be a case of mathematics predicting the hidden nature of physical reality. This is what the Platonic view of mathematics is: that abstract mathematical truths are discoverable and actually structure the physical world.
Let’s start with a quick summary of Maxwell’s 4 Laws of Electromagnetism:
in empty space, while
when there is an electric charge in space.
represents charge density, or how much charge per unit volume, while
represents the permittivity of free space, which means how much electric field you get per unit charge in a given medium. Different mediums have different
values, which were originally needed to obtain the correct equation relating electric charges, distance and force in Coulomb’s Law:
The equation says that where there is positive charge, the electric field diverges outwards (is a source), while when there is negative charge, the electric field converges inward (and is a sink), adjusted by the permittivity value of the medium we are dealing with (in this case, a vacuum).
In completely empty space with no electric field, we would get the following:
2.
This law says that the magnetic field has 0 divergence- there is no source or sink, which is unlike the case for an electric field. Magnetic fields are thus like incompressible fluids that also have 0 divergence everywhere.
3. , which is called Faraday’s Law.
This says that the electric field curls in a plane perpendicular to the axis of the changing magnetic field in time; therefore, the vector that represents this curl of the electric field points in the opposite direction to the vector representing the change in the magnetic field over time. If the vector representing the change in the magnetic field in time points upwards, then the curl vector of the induced electric field points downward, thereby representing a clockwise flow of electric current around the z axis in the xy plane. This is evident by the right hand rule. Our thumb represents the dB/dt vector, our index finger the tangent vector (del operator) to the surface in which direction we take a tiny step in , and our middle finger is E, the electric field vector. If we assume dB/dt is positive along the z axis. , we actually must point our thumb downwards, which would indicate that the electric field circulates in a clockwise direction around the Z axis.
4. , which is assumed to be in a vacuum.
Like the permittivity value, the permeability value u is the constant of proportionality that satisfies a force law (in this case the magnetic force).
In order to understand how light came to be seen as an electromagnetic wave through these 4 laws, we must first understand the mathematical basis for the identity of the second derivative of the curl, also known as the curl of curl (for more on curl, visit the previous post https://mathintuitions.com/2025/05/27/divergence-curl-and-the-taylor-series-approximation/)
The curl of curl identity is:
To derive it, let’s first label different components of the curl in the following way:
where Gx is a vector in positive x direction signifying counterclockwise curl in the zy plane, Gy is a positive a vector in the positve y direction signifying counterclockwise swirl in the xz plane, and Gz is a positive vector in the positive z direction signifying counterclockwise swirl in the yx plane.
We can now take the cross product of the del operator with the new G vector to get the curl of the G vector in space (which is actually the curl of the curl):
If we substitute our F vector values back into G, then the curl of curl in the unit vector i direction becomes:
We can add and subtract the same term (note that though written in different forms, it is still the same term; moreover, these terms have no net effect on the curl of curl), for the unit vector i direction, factor out d/dx as a common factor for 3 terms (one of which we inserted), and group the other 3 subtracted terms (one of which we inserted) to get:
Which brings us to the final expression for curl of curl, first by each component (we would repeat this same exact process for the other 2 components) and then as a whole:
This tells us that the curl of curl is equal to the gradient of the divergence of the field minus the Laplacian, or 2nd derivative curvature, of the field. This identity is what helped Maxwell to prove that light itself is an electromagnetic wave, which we will do first before delving into some other remarkable properties of the curl of curl.
To prove that light is an electromagnetic wave, start by taking the curl of Faraday’s Law (Law 3):
Faraday’s Law says:
Let’s take the curl of both sides:
Now swap the curl and time derivative on the right hand side of the equation, since they commute according to Clairut’s theorem (to understand the intuition, visit our previous post https://mathintuitions.com/2025/05/27/divergence-curl-and-the-taylor-series-approximation/ ) which says
:
so swapping the curl and time derivative yields:
Let’s now use Law 4, the Ampere Maxwell Law in a vacuum, which says
and substitute that into to get
The vector identity of curl of curl says: and in free space
, so
and the final equation is
The classical wave equation in one dimension is and in 3 dimensions is
, where c is the speed of the wave (visit https://mathintuitions.com/2025/04/28/of-unwavering-importance-the-wave-equation-derivation/ for the derivation of the classical wave equation) This is exactly the same form as:
(although unlike the classical wave equation, this equation is not constrained by the assumption of a very small angle), which implies that second order changes in the electric field travel as waves, and that these waves travel at a speed of
This speed, composed of the multiplication of the two constants Uo and Eo, is exactly equal to the speed of light. Given that only light (and other massless disturbances like gravitational waves) travel at this constant speed no matter an observer’s relative motion to it (as implied by the fact that the speed is composed of two constants), we can conclude that 2nd order changes in the electric field are actually light itself! Furthermore, because we know that electric fields generate magnetic fields and vice-versa, we can show that light is also 2nd order changes in the magnetic field, which is bound up one and the same with the electric field:
Let’s show how 2nd order changes in the magnetic field propagate as light wave too:
Starting with the Ampere Maxwell Law (#4)
Take the curl of both sides:
Use Faraday’s Law on the right hand side:
Use the curl of curl identity
Apply that the divergence of the magnetic field is everywhere 0:
to give the final magnetic field equation:
This shows that light is an electromagnetic wave made of oscillating electric and magnetic fields, which must vary with nonzero second order derivatives to satisfy the wave equation and allow propagation of the light waves. When either the electric field or magnetic field has a non zero second derivative, it generates another magnetic field or electric field , respectively, and the light wave travels as this combination.
The previous derivation is a well known and popularized derivation because of its profoundly illuminating consequences. Less well known are some of the other implications of the curl of curl vector identity, which to me seem even harder to visualize than light as an electromagnetic wave (but perhaps it is harder to visualize because it is not as popularized).
If we just take the x component alone of the curl of curl, we get:
This says that as the curl strengthens in the counterclockwise direction in the xy plane as we take a tiny step dy, we get increased counterclockwise positive curl around the x axis through the yz plane. On the other hand, if the curl strengthens in the counterclockwise direction in the xz plane, we get more clockwise negative curl around the x axis through the xz plane.
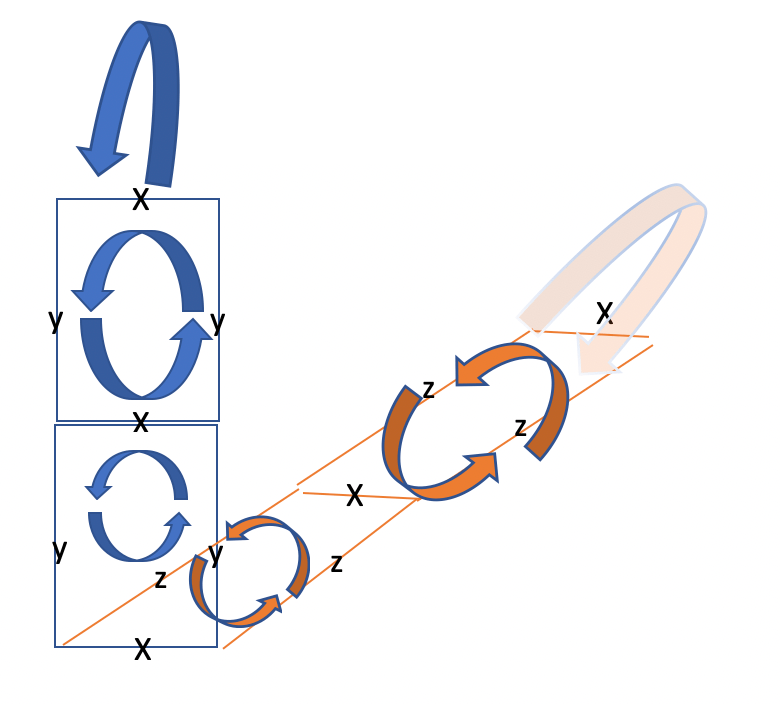
The xy plane and xz planes are experiencing increasing counterclockwise curl as you move up in y and up in z, respectively. While this increased curl causes an additional counterclockwise curl around the x axis in the first case, it causes an additional clockwise curl around the x axis in the second case. I haven’t been able to visualize why these opposite curls happen around the x-axis, but the amazing fact is that the mathematics predicts they should happen, and they do happen, even though these rotations are extremely difficult to visualize.
This observation (or my deficiency to be able to visualize) inclines me to support the Platonic view of math, which says that the pure truths of mathematics help to structure the physical world in ways that are undetectable or even contrary to our sensory perceptions. Never can I remember witnessing the curl of curl phenomenon that creates an additional rotation around an axis, yet it exists in the most fundamental parts of nature including light.
I hope this was an illuminating discussion and feel free to comment with any questions or observations to further knowledge on this subject.

Great work, Mr. Fialkow! Nothing short of tearjerking.
LikeLike
Thanks Gabe and good to hear from you! Hope you didn’t cry too hard and that all is well in college! Come back for a visit.
LikeLike