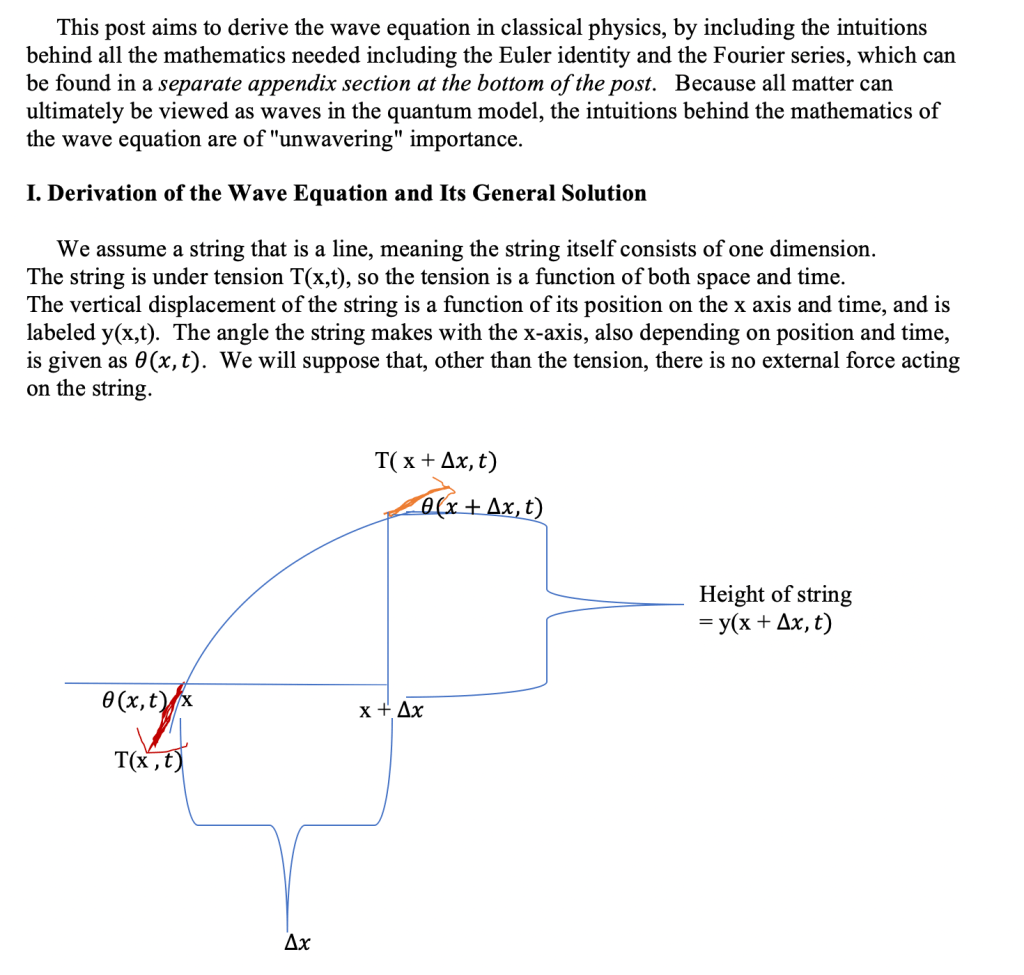
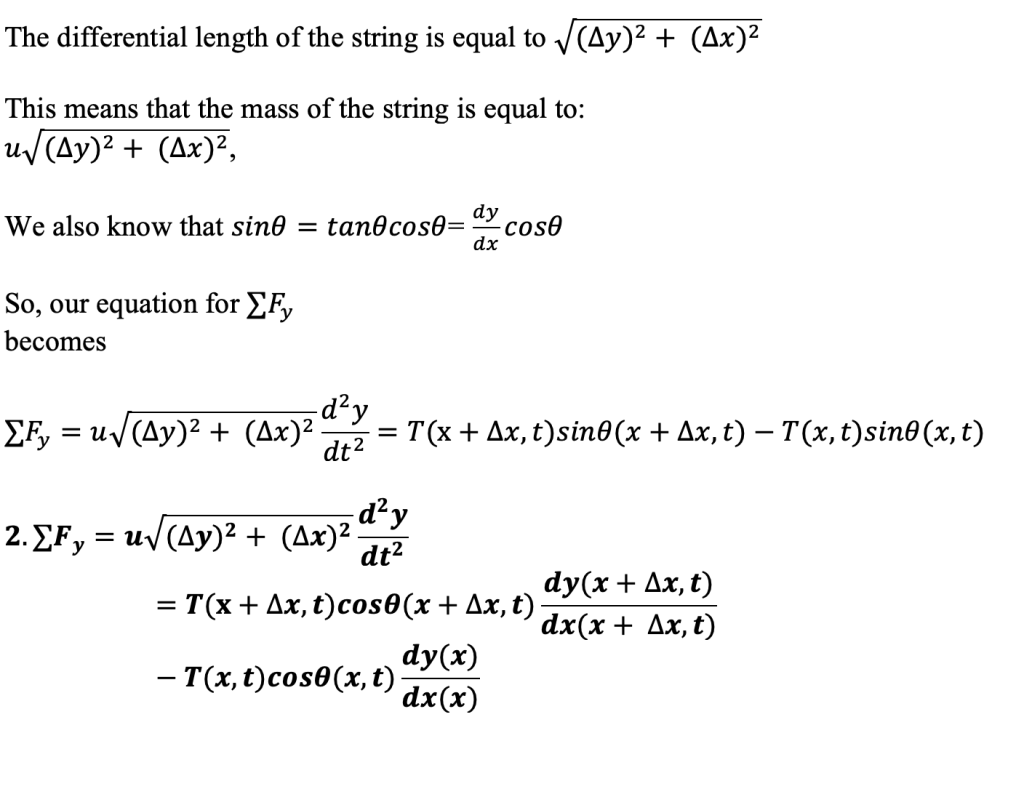
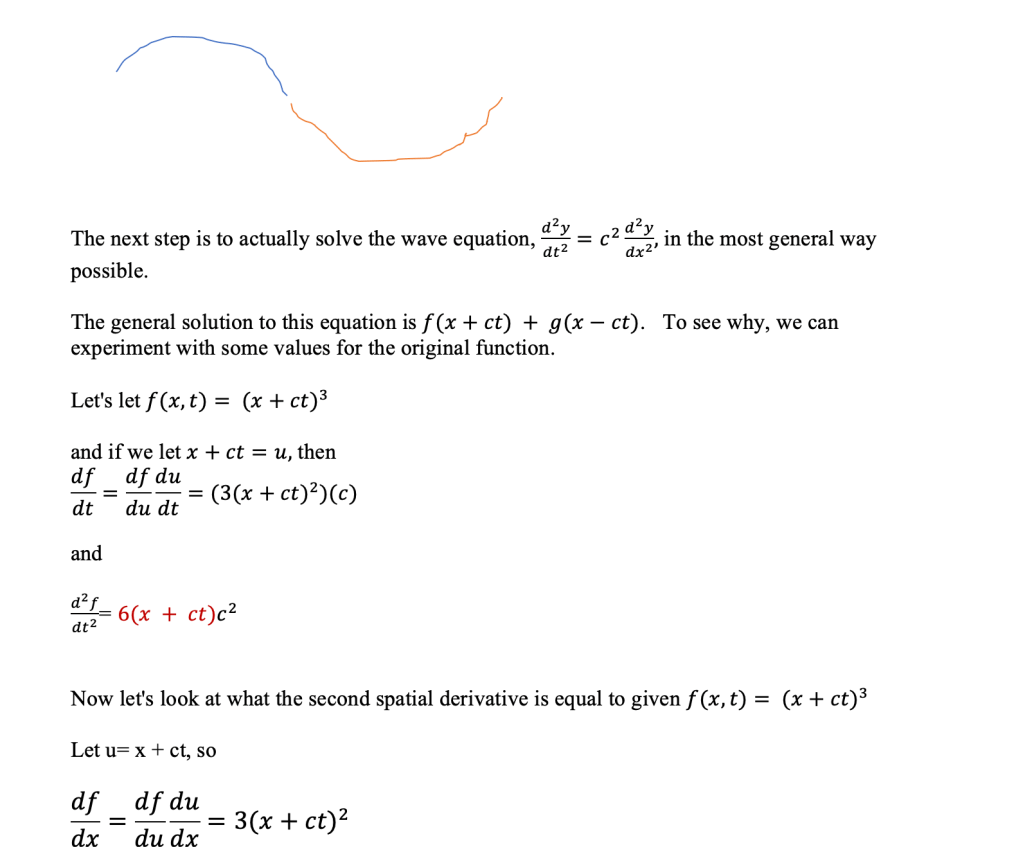
(Also, note that to achieve these boundary conditions, the sine waves across L must all be increments of half wavelengths- this is covered more in the Appendix section.)
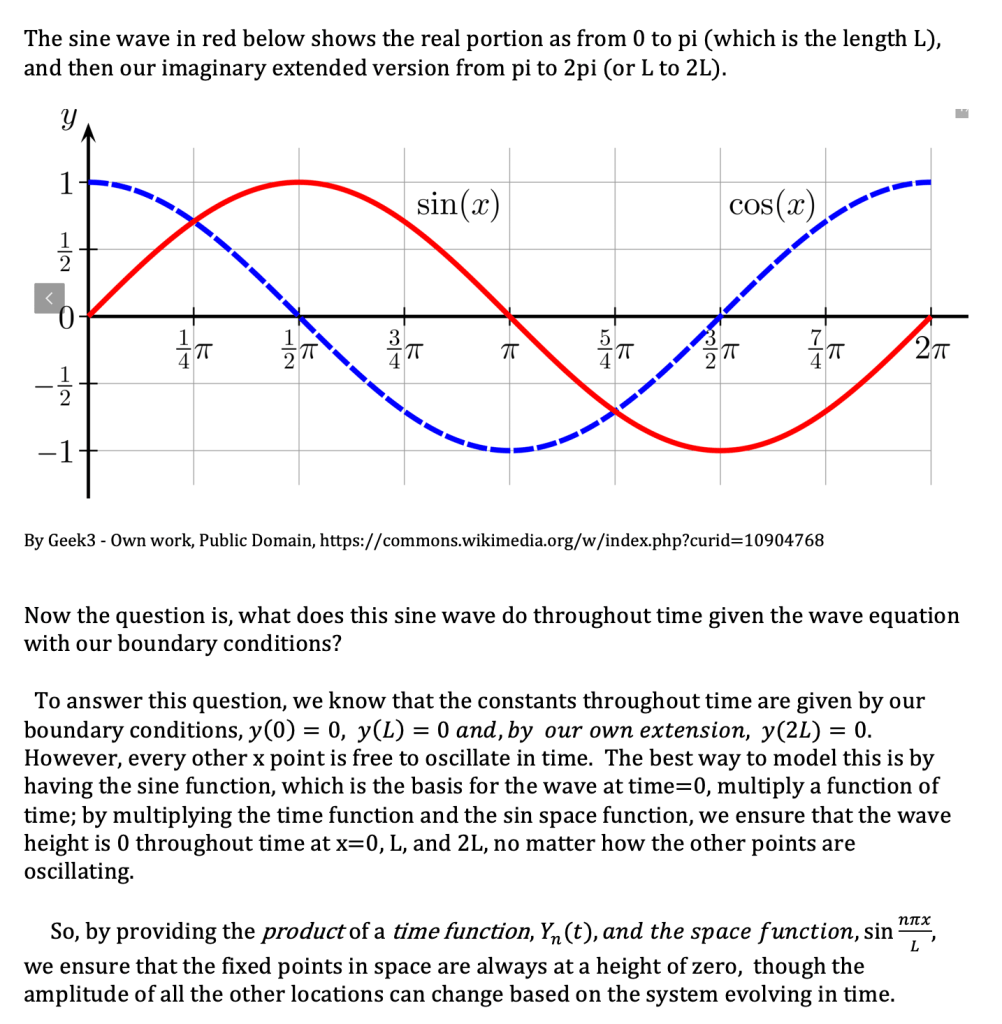
(Note: in the above the imaginary number i was dropped from multiplying the Dn coefficient. This can be done by constructing the original Cn and Dn coefficients as complex conjugates for which the i term would drop out after converting to sine and cosine, and you would obtain the purely real solution as shown above. The reason we know we can do this is because another solution of the original equation Y” + CY=0 is just in terms of sin + cos , without any imaginary numbers multiplying it.).
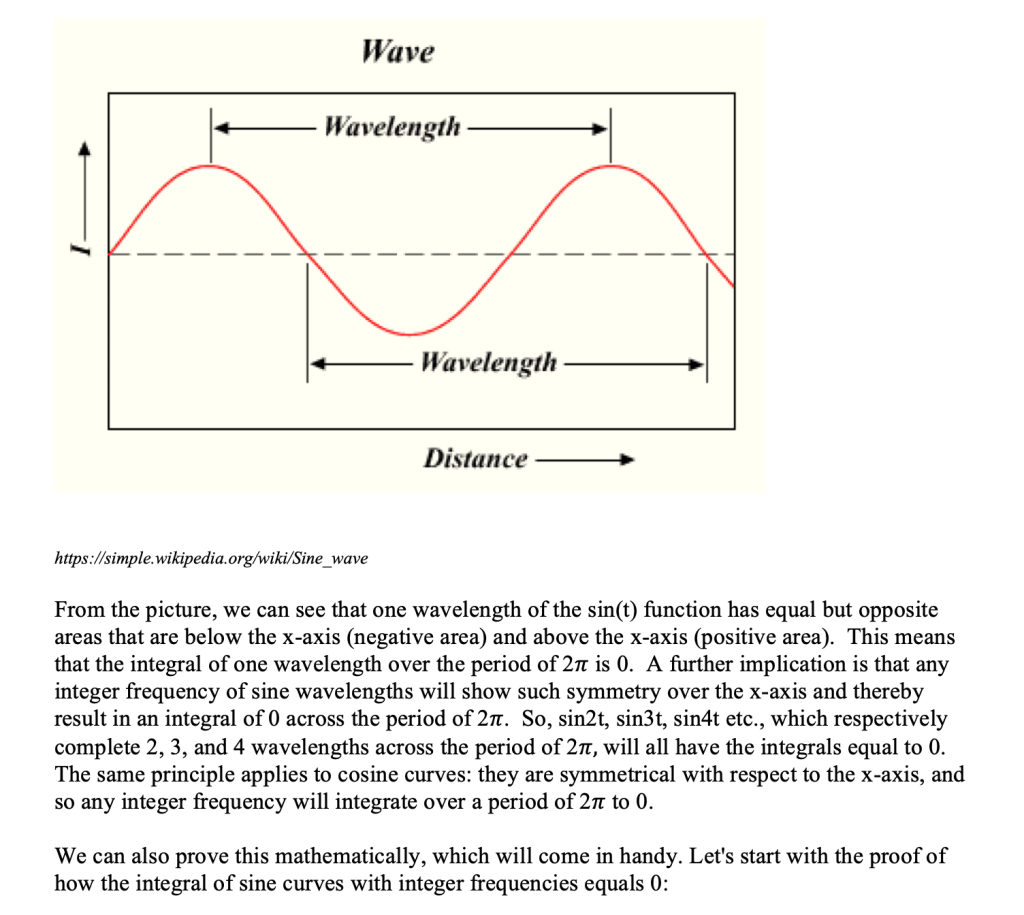
(keep in mind that it is important, that for Dirchelet boundary conditions, only increments of half sine wavelengths satisfy y(0 and L)=0.)
Mathintuitions