In many ways, the theory of relativity could have been named the theory of constancy, since it relies upon things that are invariant like the speed of light and the Lorentz factor. This post aims to derive the mysterious Lorentz factor using the fewest assumptions possible along with the most mathematical proof possible.
Before relativity came along, in order to transform between 2 different coordinate frames, the Galilean transform was used. One frame, S, the unprimed frame, measures the primed frame, S’ as moving to his right at constant relative velocity u (in the image below the relative velocity is “v” instead). The assumptions of this model are that each observer is located at the origin of his frame, measures the same rate of time starting at t=t’=0 and starting at position x=x’=0, and that t always equals t’. Additionally, if the S frame measures the velocity of S’ as u, then S’ would see the observer at the origin of frame S moving to his left at -u.
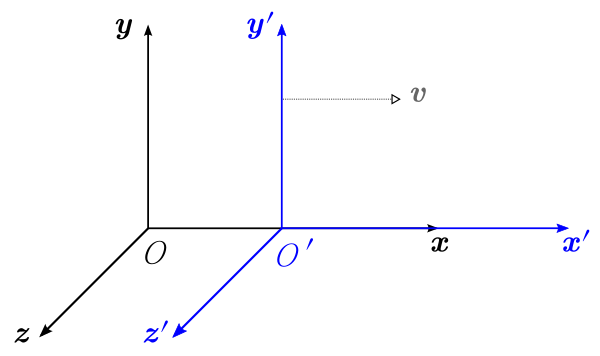
So here are the general equations describing the coordinate transformations between the primed frames (note that t is the same for both observers: Note that there is no transformation between t and t’, because both are assumed to be equal.

Now let’s also assume that the observer in S’ throws a ball to his right at t=0 and x=x’=0 . How would each frame record the velocity of the ball?
For the primed frame, the velocity would be:
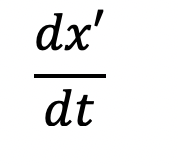
For the unprimed frame, we can differentiate the above transformation equation with respect to time to obtain:
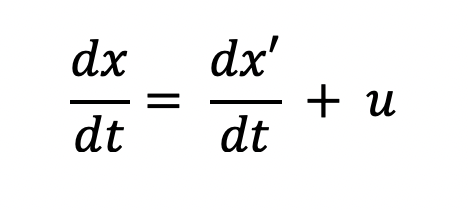
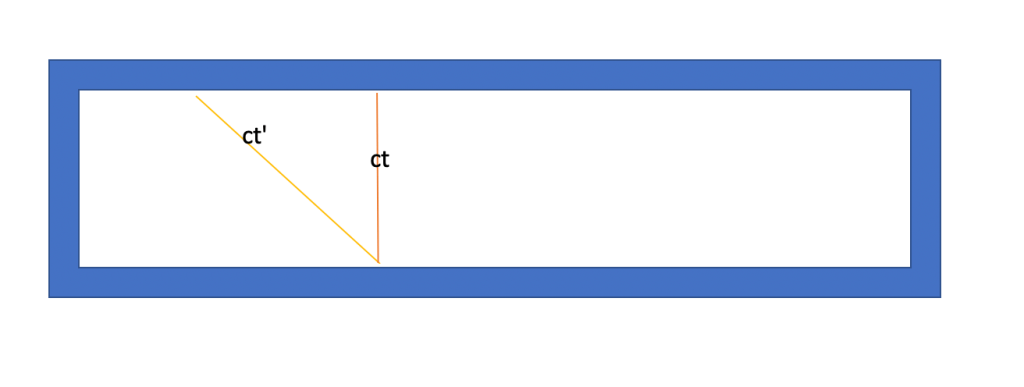
However, if instead of observer S throwing a ball he instead flashed a beam of light, we run into a major problem with the above equation. As the Michelson-Morley experiment in the late 19th century showed, the speed of light is constant at the value of c for everyone, no matter the velocity you are moving at!
This means that the equation above does not work for a light beam, since the observer at S’ would measure

but the observer in frame S would measure

which means that the observer in frame S is recording a velocity for the light beam that is greater than the speed of light, which is impossible!
We must find a different transformation between the coordinates that upholds the constancy of the speed of light, no matter the relative velocity between the frames and no matter which observer we choose. For our new transformation law, the most mind-expanding new assumption is that time in the S frame may not equal time in the S’ frame, in order to preserve the constancy of the speed of light between the 2 frames.
Like the Galilean transformation, this new transformation must be linear. In other words, for each variable input, there must be a single output that both scales in the same way as the inputs are scaled, and the different possible solutions to the equation can be added together to make a new solution For example, the equation x’= mx is linear because for any x input we choose, we get a single x’ output that is scaled by whatever x is scaled by, and whose solutions can be added to form a new solution. However, if the equation said that x’=x^2, (or any higher power), then x’ does not scale with whatever we scale x by; moreover, when x’=4 , x could be 2 or -2, which would mean that the event observed in the primed frame would happen at 4 but in the unprimed frame it would happen at 2 places at once. This clearly goes against everything we know and so we assume that the new transformation equation is linear too.
Another reason why we assume the equation is linear (and thus only to the first power of x) is to preserve Newton’s laws, which state that if acceleration is observed to be 0 in one inertial frame, it must be 0 in another inertial frame. This is intuitively true, since both observers are moving at constant velocities relative to each-other.
Let’s see why, when we assume that the frames have a quadratic relationship instead of a linear relationship, the above assumption of equal 0 accelerations is violated. We will use the chain rule to show that both x’ and x can be functions of t’:
Let’s differentiate each side with respect to t’ (which is no longer necessarily equal to t)

This also holds true for functions that are of higher powers: we would be left with dx/dt and dt/dt’ terms that could clearly be non-zero and thus violate Newton’s Laws.










Note that instead of subtracting the velocities we are adding the velocities, since according to an observer in the unprimed frame the relative velocity is positive rather than negative since he sees the primed frame moving past him to the right.
However, rather than just relying on this being true for intuitive reasons that physicists claim, I thought it important to prove mathematically since it doesn’t seem obvious to me that the equations must take the same form. I came across a great post that showed how to derive these two equations, which no longer means we need to just “trust” that they are true. It is from an author named Richard Alan, who has an excellent book. Below is the citation.
Richard Alan, Everything You Ever Wanted To Know About Dick &Jane And Mary. “The derivation of Einstein’s Special Theory of Relativity in nauseating detail”.’
He showed that by starting with the two equations below, we can mathematically derive the unprimed equations in terms of x and t.

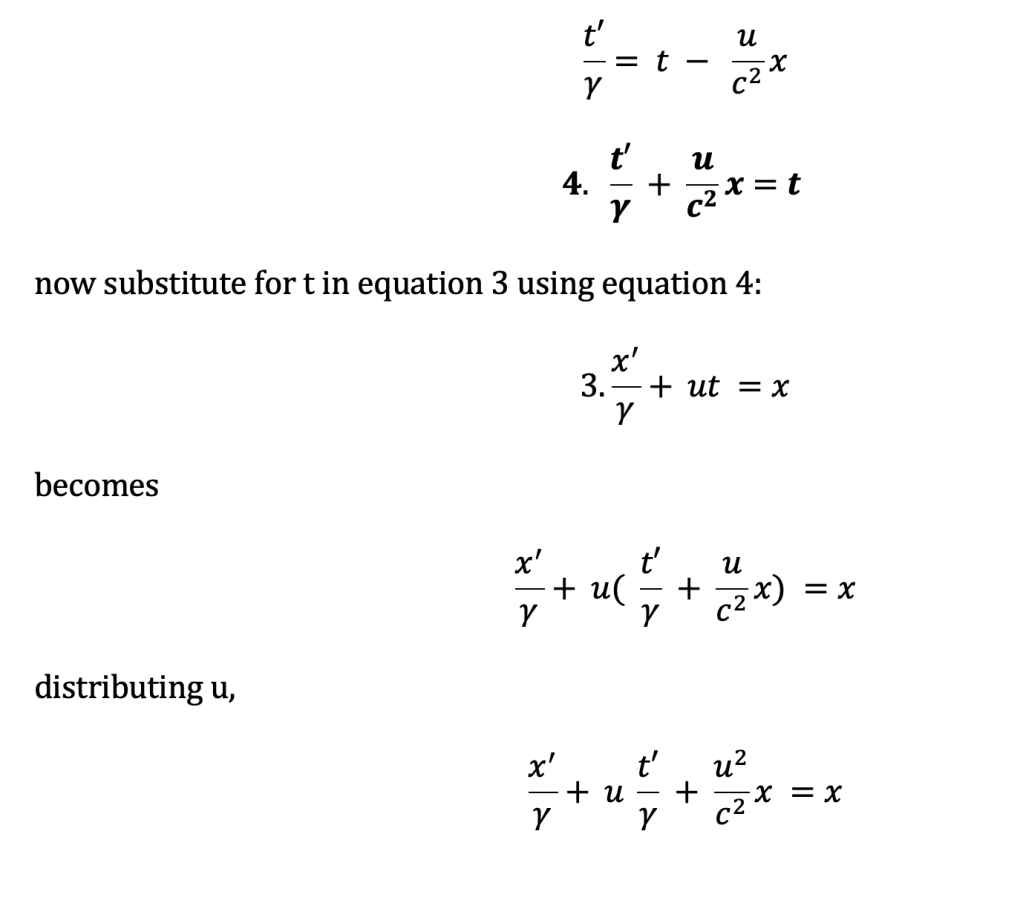

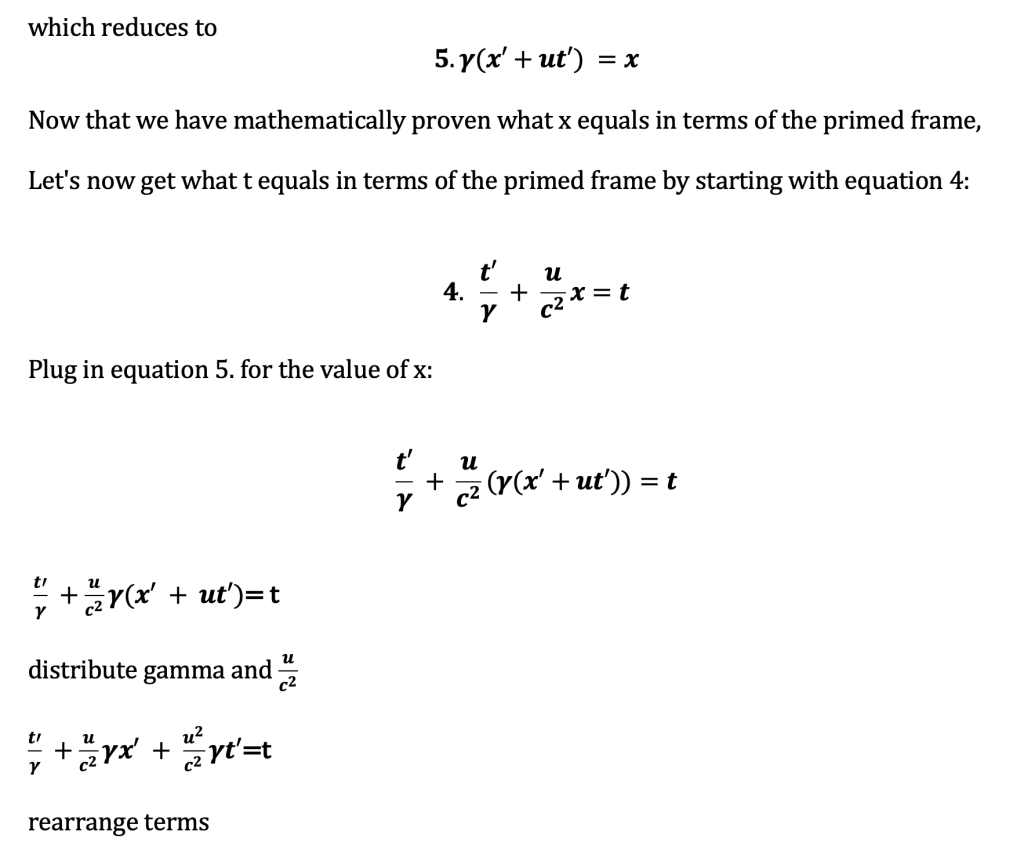

Now t is solely in terms of primed coordinates. We now have derived all four coordinate equations in terms of the other frame:
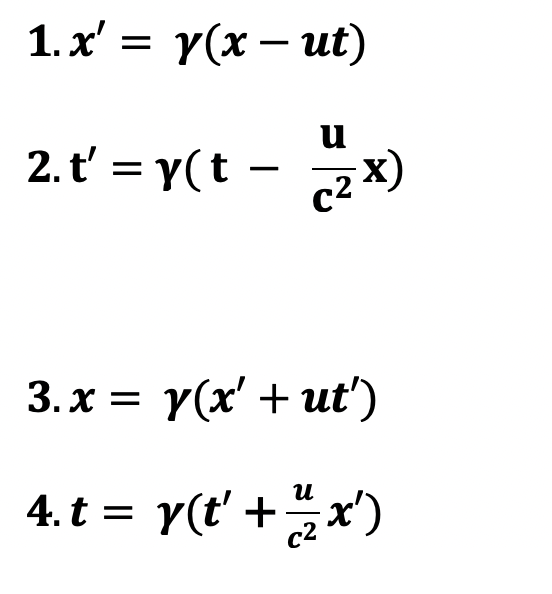
Because space and time are functions of each other, we cannot measure distance solely in terms of space alone or time alone. We want to come up with a new notion of distance in which, no matter the coordinate frame used, we would get the same distance.

Let’s see why this is invariant by showing that this equation results in the same value for both the primed and unprimed frames: Instead of dt, dx, dy and dz, we will just use t, x, y z as we will assume we have integrated across the differential. For the momet, we will also assume that there is no movement in the y or z plane so the equation reduces to:


We have just proven that, regardless of one’s inertial reference frame, every observer would measure the same spacetime distance!

This post aimed to show why the assumption of linearity was required in deriving the Lorentz factor, how we can derive the inverse Lorentz transformations using mathematical proofs rather than physical intuitions, and showing why the space-time invariant distance is truly invariant, no matter which plane the relative motion is moving though. As we have seen, the theory of relativity could’ve as easily been named the theory of constancy for all the invariants and constants involved!
There were 2 very good videos in which some of the material was drawn from and the links are presented below:
and
