In Paul J. Nahin’s book “An Imaginary Tale,” a very interesting mathematical puzzle is introduced regarding imaginary numbers that leads to connections to wormholes in the space-time continuum.
(image of wormhole is from Wikipedia AllenMcC. Vector: KES47 – Own work based on: Lorentzian Wormhole.jpg by AllenMcC., CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=30231987 ).
He discusses the discovery of American mathematician Edward Kasner, who proved that the use of imaginary numbers can result in an arc length between two points that is shorter than the straight-line distance between them. This result does not conform to the “reality” that we know of, as shown below:
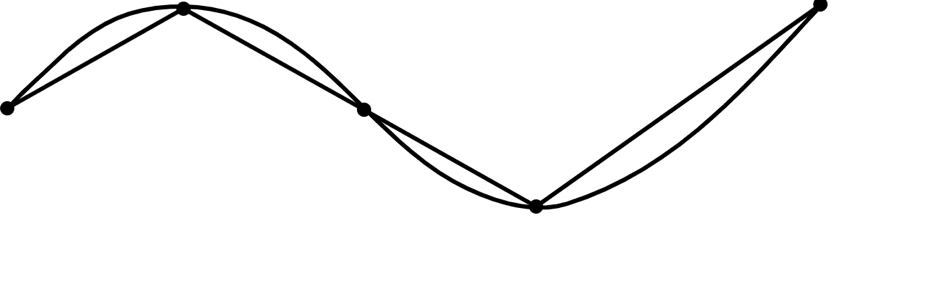
Image By Dariusofthedark at English Wikipedia – Transferred from en.wikipedia to Commons., Public Domain, https://commons.wikimedia.org/w/index.php?curid=2548423
Clearly, when connecting any two points in flat space, the straight-line distance is the shortest distance between two points (the “geodesic”), and any other function that connects the two points will result in a longer distance between them. This result does assume that we are working in a flat space rather than a curved space, just like the plane of this screen.
However, Kasner showed that the function

results in a path through which the arc length is always exactly 6 percent shorter than the straight-line distance between them.





Nahin then proposes that by changing the exponent in the equation
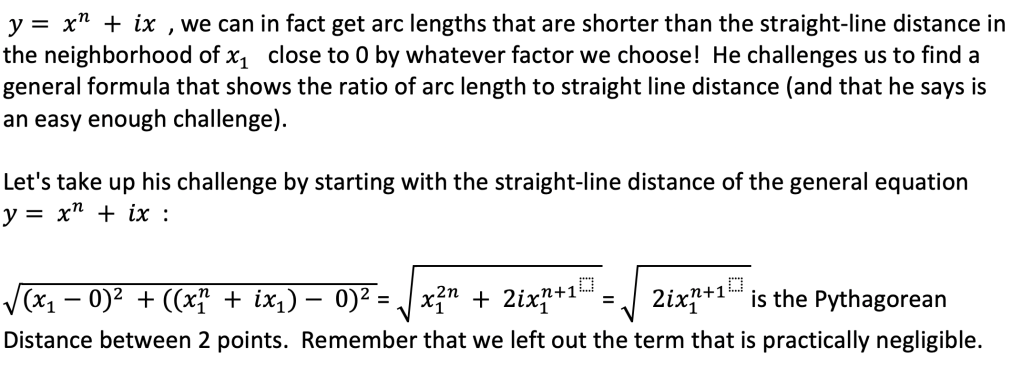


The figure below shows 2 points A and B on the surface of a cylinder. The cylinder was originally a flat piece of paper until it was wrapped around itself, so the metric on the cylinder surface is still that of flat space. The red curve connecting points A and B was originally a straight line on the flat piece of paper, and still is the geodesic living on the surface of the cylinder between the points. But once the cylinder is created, then there is a shorter route from A to B: namely through the empty space of the cylinder as shown by the blue line.
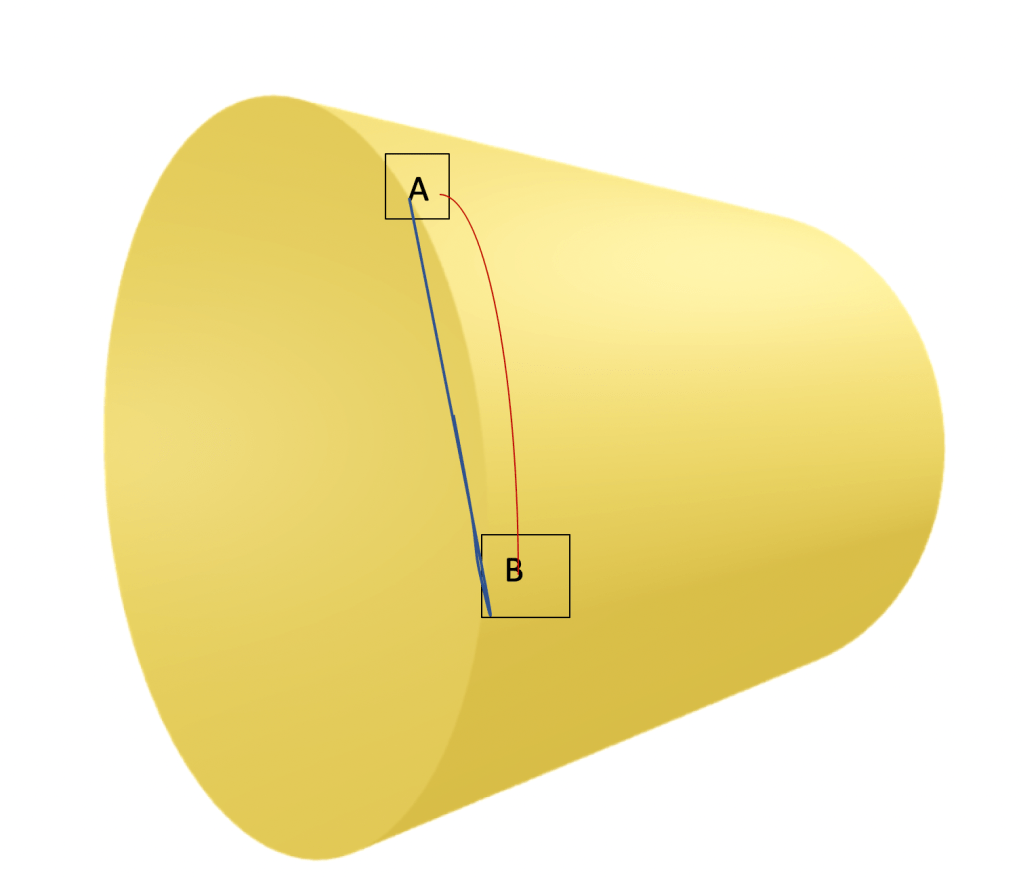
Now, we can conceivably construct a parabolic function whose arc length through the empty space of the cylinder is a given factor shorter than the straight-line distance around the cylinder. So, the ix term in our equation would not only have to account for the wrapping up of the original plane, but also account for an entirely new plane through which the function is constructed. The main issue with this line of thinking is that we are using this function for both the arc length and the straight-line distance, so shouldn’t the straight-line distance still be shorter than the arc length, since we are on the new plane for the straight-line distance too? Somehow, we would need the straight-line distance to be restricted to the surface of the cylinder or restricted in some other manner, while the arc length of the function would go through the empty space of the cylinder and be a given factor shorter than the straight line distance. Moreover, the higher the exponent, the shorter the arc length route must be when compared to the straight line distance.
This line of reasoning is analogous to the concept of a worm hole, though I am no expert on the physics or mathematics of this. Essentially, by traveling through another higher and nearly invisible dimension, we can traverse the space between two points much more quickly.
The use of the aforementioned imaginary parabolic function hints at the fact that imaginary numbers allow the mathematical possibility of such travel by finding a geodesic that is not the ordinary straight line between two points in flat space.
