From our previous discussion (https://mathintuitions.com/2022/09/22/stranger-than-fiction-a-derivation-of-the-coriolis-force-to-explain-the-path-of-hurricanes-and-snowballs-on-carousels/), the cross product of the angular velocity (with components vi and vj) with the position vector was
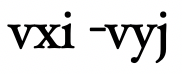
and is the tangential velocity vector. It can also be written more specifically as xivj – yjvi).
The cross product of two vectors A and B with 2 dimensions is calculated as AiBj – BiAj. From the diagram below, it is clear that vectors Ai and Bj are responsible for pulling vectors A and B at 90 degree angles to each other, while the vectors Aj and Bi are responsible for pulling vectors A and B closer together and more parallel to each other. These opposite tendencies are encoded in the formula AiBj – BiAj.
We also know that the cross product of vectors A and B represent the area of the parallelogram made by those vectors. But how can we prove geometrically that AiBj – BiAj is truly the area? This formula for the area of two vectors always made me a bit cross due to its lack of intuitive explanation, so the following question seeks to remedy that:
Question: How can we prove the cross product geometrically?
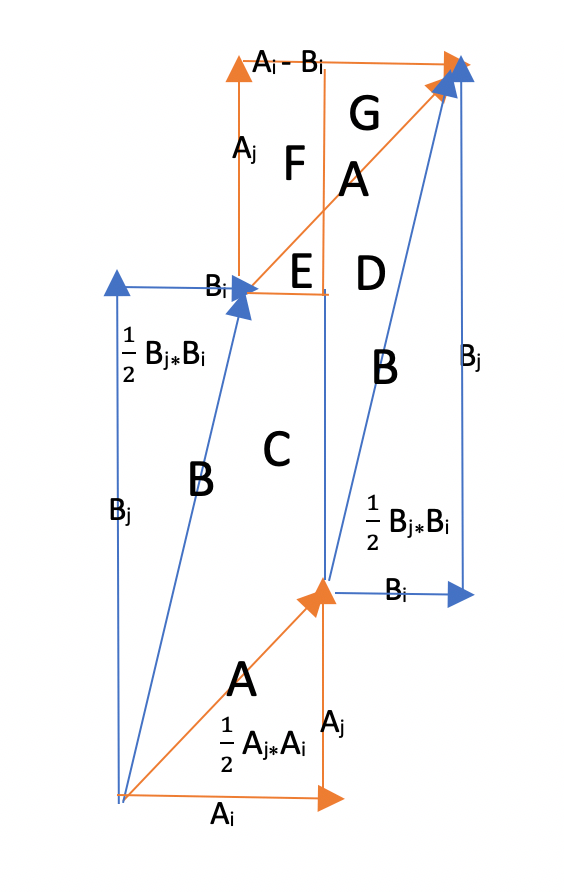

This is the cross product of two 2d vectors.
In the case of the arrangement shown above, we can use the right-hand rule to show the cross product vector is pointing up and out of the page. If we wanted to calculate, instead, the cross product of B X A, the area of the parallelogram would be the same except the vector would be pointing down into the page.
Why should the order of the cross product matter? To me, it is most evident in preserving the relationship of angular velocity, tangential velocity, and the position vector as we touched on in our previous post (https://mathintuitions.com/2022/09/22/stranger-than-fiction-a-derivation-of-the-coriolis-force-to-explain-the-path-of-hurricanes-and-snowballs-on-carousels/)

